This post aims to assist you in assessing the risk of quantum computing to your organization’s IT assets. It describes quantum computers' present and hypothetical future capabilities, and shows how various protocols could be attacked.
The second post in this series will focus on the technology available and usable today to be immune to the quantum computing threat.
0. Introduction
Quantum computers would break most of today’s public-key cryptography used to protect connections between computers and electronic devices, as well as signatures and security protocols used by blockchain platforms and many other applications. But such quantum computers don’t exist yet.
Post-quantum cryptography, immune to quantum attacks, is being developed. But it will take some time to replace elliptic-curve cryptography and RSA. Do we need to rush and adopt post-quantum cryptography? Which systems should be upgraded first? What future quantum attackers would need to do now to compromise your systems later? That’s what this post is about: the actual risks in your organization and how to plan a transition to a quantum-safe systems.
Public-key cryptography primarily serves signature, encryption, and key agreement purposes, though the quantum risk varies across applications. Transitioning to post-quantum cryptography is most crucial for encryption and less urgent for signatures, as message integrity can be preserved by issuing a post-quantum signature later, whereas confidentiality remains paramount.
There is no cause for alarm, though. You might imagine quantum computers factoring 2048-bit RSA moduli in the blink of an eye, yet as of today, experimental quantum computers can barely factor 15 into 3 × 5. Nevertheless, as the progress of science and technology is unpredictable, we have no idea when or if at all we’ll see quantum computers breaking crypto in our lifetime. We’re talking of managing a low-probability and high-impact risk, and this post offers the information to do so, namely:
- What a quantum computer is and why everybody talks about it.
- The state of the art and the achievements by quantum computing companies and researchers.
- How your systems could be impacted along with a description of how a quantum attack would work.
1. What is a quantum computer?
The quantum model of computation is a model, analogous to the probabilistic Turing Machine, in which the normal laws of chance are replaced by those obeyed by particles on a quantum mechanical scale, rather than the rules familiar to us from the macroscopic world.— Daniel Simon, On the Power of Quantum Computation
1.1. A different computing model
Quantum computers were not imagined in order to break cryptography, but for the nobler purpose of better understanding quantum mechanics. We can trace the idea of quantum computing back to, at least, the Richard Feynman’s 1981 keynote speech, which explained that classical computers are useless when it comes to simulating quantum mechanics:

Feynman’s idea lead to the development of quantum algorithms, which leverage the properties of quantum mechanics to enable a distinct computational model that can solve certain problems fundamentally more efficiently. However, quantum computers aren't universally efficient problem-solvers, and only excel at specific tasks.
A quantum computer diverges from the Church-Turing model that governs microprocessors and silicon circuits. Rather than doing a series of operations to manipulate binary bits (0 or 1), quantum algorithms alter physical entities while adhering to the principles of quantum mechanics. Instead of classical bits, quantum computers work with quantum bits (or “qubits”), which can be 0 and 1 “simultaneously”, due to the remarkable phenomenon of quantum superposition.
The other main quantum mechanical notions behind quantum computers' power are:
- Quantum entanglement, the “hidden connection” between particles, famously illustrated by the EPR thought experiment.
- Quantum interference, the property that particles can combine or cancel their effect due to their wavelike nature, famously illustrated by the double-slit experiment.
1.2. Quantum speed-up and quantum parallelism
Quantum computing processes a function on a superposition of states, which suggests quantum parallelism as the idea of calculating "all values at once." However, this intuition is deceptive, as the system operates on a single quantum state instead of a series of values. It's therefore not feasible to compute results for all inputs simultaneously and then select the "best" or most effective one, as one might do in a brute force search. The no-cloning theorem and the nature of quantum states dictate that only the answer to a problem for a single input can be determined. When a measurement is taken, the superposition collapses.
On the other hand, observing a superposition state from a different perspective allows for the extraction of alternative information, rather than merely the values on various inputs. For instance, the information gained could stem from quantum interference between entangled qubits. This enables quantum computers to accomplish specific tasks fundamentally faster than classical algorithms – not because they execute the same operations more quickly, but because they perform fewer, distinct operations. This phenomenon is known as quantum speedup.
Experts in complexity theory have a solid understanding of the quantum speedup concept. While certain computational tasks require an exponential number of operations (relative to input size) on a classical computer, some of these problems can be efficiently solved using a quantum computer (that is, in polynomial time). Consequently, a quantum computer can transform a practically unsolvable problem into a solvable one.
But only a small fraction of computationally hard problems are susceptible to such exponential quantum speedup. Specifically, quantum computers offer limited assistance in searching for optimal solutions to constraint-satisfaction problems (see NP-hard problems). Let's repeat: quantum computers are not "exponentially faster" computers that would turn any computation-intensive problem into a swiftly solvable task.
1.3. Exponential speedup: Simon and Shor
Simon’s algorithm, introduced in 1994, was the first to demonstrate exponential quantum speedup. It addressed Simon’s problem: given access to function f(x) mapping n-bit values to n-bit values, find the secret string s such that f(x) = f(y) if and only if x ⊕ y = s. Classical algorithms require O(2n) operations to solve this problem, an exponential cost that becomes practically unattainable as n grows greater than (say) 100. In contrast, Simon's algorithm solves the issue in O(n) time, a linear cost proportional to the string size, making otherwise impossible cases solvable.

Simon's algorithm inspired Peter Shor to develop Shor's algorithm in 1994, which showcased a quantum computer's ability to factor large integers exponentially faster than classical computers. Namely, in cubic time O(n3), where n represents the size of the number in question. Shor's algorithm tackles problems that underpin most of today's internet and IT security:
- Factoring: given a number n = p × q, find the prime factors p and q. If you can solve this problem, then you can break the RSA cryptosystem and a number of related ones, such as Paillier's, used in some e-voting and zero-knowledge proof systems.
- Discrete logarithm: given a number y = gx mod p, find x when you know the other numbers. If you can solve this, then you can break most of elliptic-curve cryptography (ECDSA, elliptic-curve Diffie-Hellman, many advanced protocols, etc.).

Many of the currently deployed cryptography protocols depend on the hardness of one or both of these problems, making quantum computers a potential threat. They could break numerous cryptographic algorithms and protocols currently safeguarding the confidentiality and integrity of our information systems. HTTPS connections? Dead. Bitcoin and Ethereum? Dead.
Furthermore, in 1996, the development of Grover’s algorithm for searching an unsorted database introduces the amplitude amplification trick and was thought to provide a quadratic speedup over the best classical algorithm. This is expected to reduce the security of symmetric ciphers such as AES. For example, with a 256-bit key, Grover's algorithm could theoretically recover the key with of other order of 2128 operations. However, executing such an algorithm would be far more resource-intensive than performing 2128 classical operations.
These advancements have significantly contributed to complexity theory, which examines the difficulty of solving computational problems by quantifying the necessary resources. Quantum computing has paved the way for exploring problem complexity and the potential for quantum speedup.
As of now, there is no functional quantum computer capable of tackling cryptography, but it may become a reality within the next few decades. To better understand the state of the quantum computing offering and the cryptographic schemes at risk, we must delve into these questions further.
2. State of the art research and engineering
The aforementioned theoretical breakthroughs have piqued the interest of major tech companies and research institutions, drawing them into the realm of quantum computing. Let’s review what “building a quantum computer” actually means.
2.1. Development of a quantum computer
A useful quantum computer would have to be:
- Fault-tolerant, if it can operate correctly in spite of the errors that occur internally due to the physical components' fragility and sensitivity to their environment. Quantum error-correction codes play a major role in ensuring fault tolerance.
- Universal, if it is not limited to a specific algorithm or set of problems, but can run arbitrary circuits and thus arbitrary quantum algorithms provided by its users.
- Scalable, if the resources required do not grow exponentially in regards to the target error probability of the observed result.
Contemporary quantum devices are inherently noisy, and observing a quantum system inevitably introduces unmanageable noise and disrupts the state. Present advancements aim to incorporate quantum error correction and fault tolerance, ensuring accurate and prolonged operation of these devices.
There are different approaches and technologies used to represent a qubit in order to try and develop a fault-tolerant universal scalable quantum computer, which fall in two main categories:
- Superconducting qubits: Constructed from superconductor materials, these components were first demonstrated as viable qubits in 1999. Major companies such as IBM, Google, and Rigetti actively conduct research in superconducting quantum computing. In 2019, Google unveiled the Sycamore chip, a 54-qubit superconducting transmon quantum processor used for the largest chemical simulation on a quantum computer. Despite being the most widespread and developed platform for quantum computing, superconducting qubits have drawbacks, such as increased sensitivity to quantum noise and stability challenges.
- Trapped ion qubits: This technology encodes qubits in the internal energy states of ions, which can be manipulated using laser pulses. As a promising platform for quantum computing, the company IonQ introduced a commercial trapped-ion quantum computer in 2018, with over 60 two-qubit gates and 11 qubits. In 2021, researchers achieved the first entangled gate between two logical qubits encoded in topological quantum error-correction codes using a 10-ion trapped ion quantum computer.
Additionally, photonic qubits are an area of significant research, leveraging the quantum state of photons for encoding and processing quantum information. In 2009, researchers at the University of Bristol demonstrated Shor's algorithm on a silicon photonic chip.
Other technologies, such as topological qubits and Rydberg atom qubits, continue to be active research areas in the pursuit of a universal quantum computer. Regardless of the technology employed, the development of a universal quantum computer will profoundly impact current protocols. For a more detailed look at the history of quantum computer engineering, refer to these two timelines.
2.2. Counting qubits: caveat emptor
When evaluating quantum computing technologies, it is crucial to draw certain distinctions to avoid misconceptions. First, a key differentiation lies between physical and logical qubits. Physical qubits represent the actual quantum system's number of qubits, while logical qubits are a subset of physical qubits used as a single, often error-corrected, qubit during computation. An example ratio may be of the order of 1,000 physical qubits to 1 logical qubit, depending on the technology used.
Such a ratio arises from the fragile nature of qubits. Different technologies possess unique advantages. Superconducting qubits, although most prevalent in quantum computing research, maintain their state for a brief period in the current experimental setups – microseconds to milliseconds – and require isolation due to their sensitivity to environmental noise. On the other hand, trapped ion qubits have a longer coherence time of several minutes, are more resistant to environmental noise, but are difficult to scale up. Moreover, qubit gate applications have an error probability of around 1%, posing significant computational challenges.
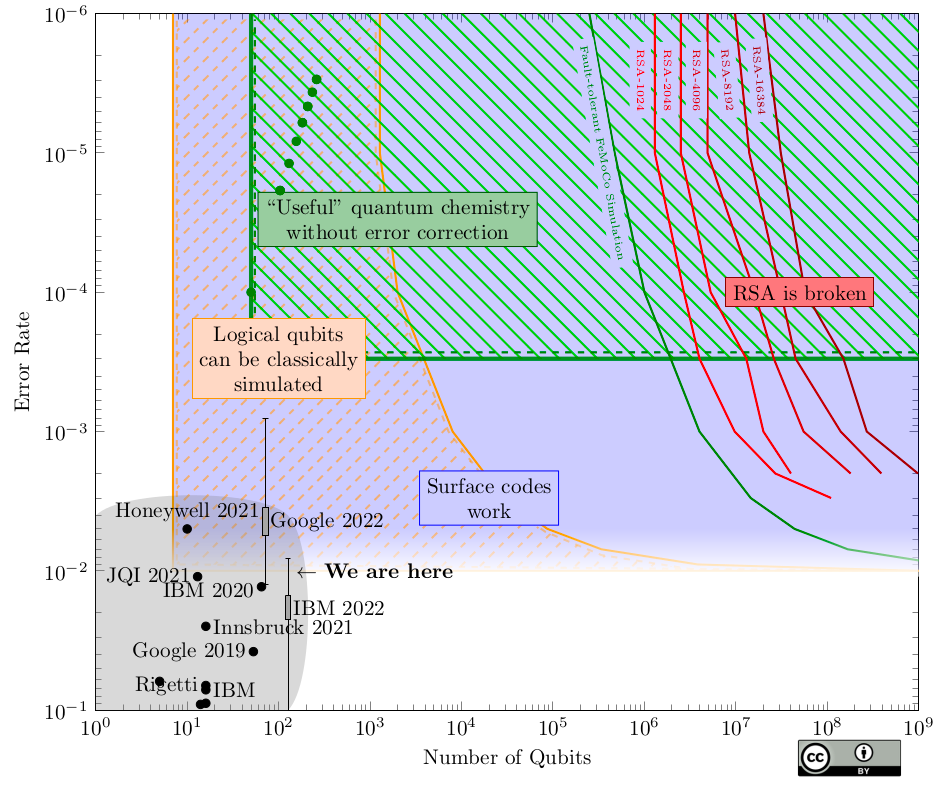
By understanding these distinctions, we can gauge our distance from the quantum cryptography threat. To break RSA-2048, we would need thousands of logical qubits, translating to millions of physical qubits, and more than 2 billion consecutive gates (according to today’s estimates).
Given our current advancements, as illustrated in the graph below, it is evident that we are far from facing imminent risks. Exponential improvements are necessary to achieve more and better-quality qubits. A detailed explanation of the graph can be found here. (Image credit: Samuel Jacques in Quantum Landscape 2022.)
2.3. Other types of quantum computer models
Quantum device that are not full-fledged, scalable universal quantum computers may be less powerful and versatile, but may not be useless either. Let's review two classes of such systems.
Noisy intermediate-scale quantum (NISQ)
The main obstacle is the quantum computing technology itself and how to maintain a quantum state. In 2018, John Preskill authored a paper in which he introduced the concept of Noisy intermediate-Scale Quantum (NISQ) and assessed the current state and future potential of quantum computing.
The term "intermediate scale" refers to quantum computers with qubit counts ranging from 50 to a few hundred qubits, which already surpasses the simulation capacity of the most advanced digital supercomputers. However, the inherent noise in these quantum computers presents a significant constraint on their capabilities. Simultaneously, there is a tradeoff to consider, as making a quantum circuit more resistant to noise might also render it more susceptible to classical simulation.
Quantum annealing
Simulated annealing is an optimisation method that was invented in the early 1980s inspired by metal annealing. However, the method often returns local minima instead of global minima for many applications.
In January 2017, the company D-Wave introduced the D-Wave 2000Q system, a 2000-qubit quantum device. Rather than being a circuit-based quantum computer, it is a so-called quantum annealer. Quantum annealing is a noisy variant of the Quantum Adiabatic Algorithm introduced in 2000. Such systems cannot execute arbitrary programs, nor can they run quantum algorithms that offer superpolynomial quantum speedup, such as Shor's algorithm.
Quantum annealing capitalizes on the ability of quantum particles to tunnel through barriers and escape local minima. Although noiseless adiabatic qubits are theoretically as powerful as circuit-based quantum computing, they entail a significant overhead cost, and the scalability of quantum annealers remains unproven. Further experimentation is necessary. More broadly, no scientific evidence currently supports the cost-efficiency of these machines compared to classical systems.
For an expert perspective on this subject, refer to Scott Aaronson's 2015 blog post.
3. How to break security protocols with quantum computers
When assessing the risk of quantum computing against your information system, it is essential to remember that today's security protocols protect information that must remain confidential for a specific period in the future. Therefore, if an adversary intercepts and stores encrypted messages today, they could potentially decrypt them if quantum computers appear in the future.
In the following, we attempt to go beyond the “secure vs. not secure” summary, by comparing the actual operational constraints and effort required to compromised common security protocols, in terms of data interception and (quantum) computation.
3.1. TLS / HTTPS

Transport Layer Security (TLS) is widely considered the most critical internet security protocol. It safeguards connections to websites through mobile or desktop browsers (via the HTTPS protocol) and is broadly employed in client-server or machine-to-machine communication scenarios. For instance, TLS is used by mobile apps interacting with back-end servers, email relay servers, many VPN services, and cloud infrastructure systems, among others. In the following analysis, we will concentrate on TLS 1.3, the most recent version of the protocol.
How does it work?
In its most common setting, TLS uses a combination of public-key and symmetric cryptography, to respectively determine the session secret keys and protect the data. These two parts are called the Handshake protocol and the Record protocol, and work as follows:
- The Handshake protocol enables the client and server to negotiate security parameters for a connection and to establish keys for the Record protocol. Typically, the client initiates the connection by sending an ephemeral public key (a.k.a. key share) encrypted using the server's public key. In response, the server provides an ephemeral public key. Both parties then derive the session keys and an initial value (IV) from the Diffie-Hellman shared secret. During the Handshake, public-key cryptography is used for signatures and (elliptic-curve) Diffie-Hellman key agreement.
- The Record protocol ensures the confidentiality and authentication of application layer data using keys derived from the Handshake protocol. Employing authenticated encryption with associated data (AEAD), the protocol takes a 64-bit nonce formed of the XOR between the client (or server) IV and a sequence number. This number is initialized to zero and incremented for each record.
The quantum attack
The threat model we consider is an active attacker eavesdropping on the communication between the client and the server while capturing all messages and potentially modifying them.
A quantum computer enables an attacker to extract private keys from public ones, namely the ephemeral key sent by the client, and the long-term public key of the server. They can thus directly recover the shared secrets, and thus session keys and IVs.
To decrypt a given (encrypted) record, the attacker needs to know the nonce, and thus the sequence number. This requires only the records count or an educated guess. If there is complete uncertainty about the number of records processed, Grover's algorithm can potentially assist in bruteforcing the nonce, which may be quite inefficient.
In conclusion, the attacker mostly needs to have captured the handshake messages. However, the attack may be non-trivial if little to no information is available on the number of records processed.
3.2. Signal protocol / end-to-end encryption

End-to-end encryption (E2EE) is a method used to secure data between two users such that it prevents any third party from decrypting the data sent from one endpoint to another. Third parties include app owners, service providers, etc. An E2EE protocol that uses the open-source Signal Protocol has the particularity of providing perfect forward secrecy.
How does it work?
There are two sub-protocols to the Signal protocol : the X3DH key agreement and the Double Ratchet algorithm. Both of which rely on the Diffie-Hellman key-exchange.
- The Extended triple Diffie-Hellman key agreement (X3DH) combines four key pairs (longterm and ephemeral), including one-time “pre-keys” are used to simulate online-ness. X3DH provides forward secrecy and requires out-of-band identity verification (via safety numbers verification). It is then secure against a malicious server, for example.
- The Double Ratchet protocol computes message-only keys in order to guarantee forward secrecy even when the shared secret key gets compromised. This is done by having a new Diffie-Hellman for each first message from a party and deriving subsequent keys from the hash of the previous key.
The quantum attack
The threat model we consider is an active attacker eavesdropping on the communication between the client and the server while capturing all messages and potentially modifying them, by having compromised the messaing server. We assume that the parties have verified their safety numbers (otherwise, Signal is not secure, even against classical computers).
Note that a network attacker not having compromised the server would need to break the link encryption between peers and the server. This protocol is TLS (via WebSocket) for Signal, and a Noise version for WhatsApp; both of which can be attacked by quantum computers.
Similarly to TLS, the risk lies in the potential for a quantum computer to break the asymmetric encryption algorithms used. Both X3DH and the Double Ratchet subprotocols rely heavily on the Diffie-Hellman key exchange, broken by Shor's algorithm. Note however that the Signal protocol does not use signatures.
Unlike TLS, however, in order to decrypt a given encrypted message, the attacker needs to intercept and capture all of the session's messages that came before it, because of how keys are derived by the double ratchet protocol. For slightly more detail, see this 2016 blog post by Frederic Jacobs.
3.3. 4G and 5G communications
4G and 5G are the two latest generations of cellular networks, which use cryptography for authentication and content protection. Unlike the previous protocols, public-key cryptography is generally not used, but does it guarantee that the protocols are quantum-safe?
How does it work?
A session such as a phone call starts by the authenticated key agreement (AKA) protocol. This relies on a symmetric key shared between the user (stored in its SIM) and its home network provider (stored in its authentication center). This key is generally of 128 bits.
In more detail, the authentication protocol involves three main parties: the user equipment (UE), a serving network, and a home network. Each network generation defines authentication methods: "4G EPS-AKA" is based on a shared symmetric key, that is also case for "5G-AKA" except that the UE always uses the public key of the home network to encrypt the UE's permanent identity before it is sent to a 5G network. In 4G, the UE always sends its permanent identifier in cleartext to the network.
The AKA protocols of 4G and 5G are otherwise similar. Using only pseudo-random functions (a symmetric-key primitive, quantum-safe), they proceed to mutual authentication and determine shared symmetric keys. These keys are then used to protect the confidentiality and integrity of the payloads, still using symmetric algorithms.
5G defines another authentication method called EAP-TLS, which supports public-key cryptography-based authentication for UE, for limited use cases such as private networks and IoT environments, in order to avoid the power and space constraint of a physical SIM.
Note that the VoLTE standard relies on similar symmetric-key mechanisms as the AKA, and has been demonstrated to be insecure (against classical, non-quantum attacks) under certain circumstances.
The quantum attack
All protocols used in 4G and 5G to determine session keys are based on symmetric key sharing, and do not use public-key cryptography. They are therefore not subject to quantum attacks using Shor's algorithm, and the encrypted data streams could not be decrypted. However, a 128-bit symmetric key could allow for quantum attacks leveraging Grover's algorithm, and thus reduce the security level to a value between 64 and 128 bits. But such an attack would be costly and slow, as it would require implementing 4G/5G's pseudo-random functions as quantum circuits.
5G's protection of the UE permanent identifier could however be defeated, as it's using public-key encryption. These encrypted identifiers may be collected and decrypted in the future, once quantum computers are available. This attack does not apply to 4G, as it leaves such identifiers in clear text.
Among the protocols discussed, only the EAP-TLS version is clearly not quantum-safe, as it relies on public-key cryptography.
3.4. Blockchains and smart contracts
Blockchains are used as a platform to exchange various types of assets, from cryptocurrencies such as bitcoin and ether to NFTs and tokenized securities. They are also the operating system of countless decentralized applications, such as decentralized finance (DeFi) systems and marketplaces. The value at stake is huge, making blockchains an attractive target for attackers, including future quantum attackers.
How does it work?
The crux of blockchains' security, as far as pure cryptography is concerned, are signatures: each account has a public/private key pair, where the private key pair is the only value needed to "unlock" the assets owned by the account, and more generally to issue transactions on behalf of the account.
The second security-critical protocol is the consensus mechanism between nodes of the network. This is a multi-party protocol using cryptography for various purposes:
- Communication between nodes must be authenticated, which requires some form of public-key infrastructure and secure channel protocols, for example libp2p.
- Consensus protocols also typically involve signatures as well, with algorithm that may differ from those used for signing transaction (for example, Ethereum validators use BLS signatures rather than ECDSA).
- Protocols based on a proof-of-work (PoW) involve repeated hashing, thus without public-key cryptography. An exception is Aleo's proof of succinct work (PoSW), where the work that is proven is the generation of SNARK proofs.
The quantum attacks
An overwhelming share of blockchain platforms use elliptic curve-based signatures (ECDSA or EdDSA), rather than post-quantum schemes. Those would therefore be broken by a quantum computer. However, there is no need to rush a transition to post-quantum signatures – unlike with encryption, security can be salvaged by migrating to post-quantum constructions in due time.
Regarding PoW, note that hash functions are fairly quantum-resistant – their security would only degrade from Grover's quantum search algorithm, which facilitates the search for n-bit preimages. However, most cryptographic hash functions are used with an output of 256 bits or more, leaving a large enough security margin.
However, consensus protocols' network communications would be compromised, as well as endorsement mechanisms that use public-key signatures such as ECDSA.
3.5. Zero-knowledge proof systems
Zero-knowledge proof of knowledge protocols, a.k.a. ZK proof systems, allow a prover to convince a verifier of a statement that is efficiently verifiable, yet without revealing said statement, and in the form of a piece of data of small size (the “proof”). Such a statement can be the solution to a hard problem (say, discrete logarithms), or “I know a solution to the following equation”. Researchers have created such efficient, general proof systems, and also found techniques to translate “business/application logic” (such as, “the smart contract or transaction was correctly executed”) into mathematical “I know a solution to this equation” terms, so as to apply ZK proofs to their applications.
As of today, the main applications of ZK proof systems are in blockchain platforms, where they’re used for two use cases:
First, private transactions, whereby the transaction type and data is hidden, for example:
- Private transfers, à la Zcash or Monero, where the sender, recipient, and value transferred are hidden.
- Private smart contracts, à la Aleo, where the smart contract executed (and its input values) are hidden.
Second, for scalability, in “ZK rollups” protocols, which aggregate multiple transactions (that is, smart contract executions that modify the state of the system), and prove that the new state was correctly computed (albeit without necessarily guaranteeing the secrecy of the underlying data). Such protocols include for example Aztec, Polygon Hermez, StarkNet.
How does it work?
ZK proof systems involve a number of cryptographic building blocks, such as signature schemes, commitment schemes, homomorphic encryption schemes, secret-sharing schemes, and so on. Many constructions of ZK proof systems ultimately rely on the discrete logarithm problem and/or the factoring problem. Certain ZK constructions, such as STARKs, however, only rely on hash functions and components that would withstand quantum attacks.
For examples of state-of-the-art ZK proof systems, see the HyperPlonk and HyperNova constructions (not all such schemes use the prefix "Hyper" though).
When it comes to the security of ZK proof systems, three complementary notions apply:
- Completeness: if the statement is true, an honest prover can convince an honest verifier that the statement is true.
- Soundness: if the statement is false, a cheating prover cannot convince an honest verifier with very high probability.
- Zero-knowledge: if the statement is true, no verifier learns anything other than the fact that the statement is true.
The quantum attacks
If the ZK proof relies on public key cryptography then it would become vulnerable to quantum attacks and the security of the proof could be compromised. This would mainly lead to the following exploitation scenarios:
- Compromise of soundness, allowing an attacker to forge proofs for invalid statements, for example to transform money they don't own, or for performing other unauthorized operations.
- Compromise of zero-knowledge, allowing an attacker to extract information from proofs, potentially exposing sensitive data.
Note that a soundness compromise would only possible against a live, running network, whereas a zero-knowledge compromise can target previous transactions, even after a network has upgraded to post-quantum cryptography.
3.6. VPN technologies
Historically, virtual private network (VPN) technology allowed users to establish a secure connection to a corporate or institutional network. Today, VPNs are also used to establish a proxy when connecting to internet to hide one's address. Many such services are commercially available, many of which rely on TLS (including those based on the ubiquitous OpenVPN suite), but IPsec and WireGuard are also common. Note that we also often talk of "VPN" when connecting to a remote host via a secure protocol, in similar way as SSH tunnels. For such applications, IPsec and WireGuard are more common, depending on the use case type and industry.
Let's examine more closely these three classes of protocols:
TLS-based
All traffic between a browser and a TLS-based VPN is usually encrypted using the TLS protocol (though not necessarily in its latest version, 1.3) and does not require any complex configuration. The security of a TLS-based VPN relies fully on the security of the TLS protocol, therefore the same attacks are possible as those seen in section 3.1. That is, an attacker having recorded the TLS handshake messages could, after having computed the private key and from that the shared secret, decrypt the Record protocol messages, as long as they can predict the sequence number.
IPsec-based
VPNs are the main use case for the IPsec protocol suite. IPsec is versatile but tend to be more difficult to setup compared to TLS or WireGuard. Today, the key agreement (equivalent to TLS's Handshake protocol) is generally done through the Internet Key Exchange protocol version 2 (IKEv2), which does Diffie-Hellman operations. This determines the session keys used by the Encapsulating Security Payload (ESP), which uses symmetric cryptography (typically, AES-GCM) to protect the content transmitted. As TLS, the key agreement is the weak link as far as quantum attacks are concerned.
WireGuard-based
WireGuard is a more secure channel protocol, which unlike TLS or IPsec does not let the user pick their own, potentially weak cipher suite. Instead, it builds on thoroughly chosen primitives and subprotocols. WireGuard's key agreement uses the Noise_IK Diffie-Hellman handshake pattern (with the 256-bit curve Curve25519) to establish session keys in one round trip. It then protects content using symmetric primitives (ChaCha20 and Poly1305). WireGuard is known for its small codebase, high performance and supporting many security properties such as identity hiding and DoS attack mitigation.
The security is once again mainly based on the security of the Diffie-Hellman key exchange which becomes obsolete in the face of an attacker with access to a quantum computer. If an attacker manages to get a hold of a public key, they could then derive the corresponding secret key and from it the shared secret used to encrypt the messages. However, note that WireGuard will not expose a peer's public key to anyone: to attempt to connect to a given peer, one must already know its public key.
WireGuard also includes a pre-shared key (PSK) as an additional argument of its key agreement. Set to zero by default, this value can be set via an out-of-band channel or a post-quantum key exchange mechanism in order to alleviate Diffie-Hellman's vulnerability to quantum attacks. With such a PSK as a safety net, WireGuard retains some quantum resilience.
4. Conclusion
Many security protocols that we use are fundamentally not quantum-safe, but not all would be equally easy to attack, would a scalable, efficient quantum computer ever come out of the research labs – which we do not expect until at least 30 years. When assessing the risk for your organization, it's also important to consider the following factors:
- How valuable are your assets on for how long to they need protection?
- How long and costly would it be to migrate your systems to post-quantum technology, would the risk materialize faster than anticipated?
- Do you have a comprehensive, documented review of all your cryptography use cases, including potentially proprietary techniques?
- To what extent do you rely on the cryptography of your suppliers?
To further help you navigate this unique threat landscape, our second post will describe what are the concrete options offered today by technology providers, and what standardization initiatives exist to facilitate the deployment of interoperable, certified post-quantum cryptography.